انواع زاویه
در علوم سوم و چهارم دبستان انواع زاویه توضیح داده شده است که در این مقاله کامل توضیح خواهیم داد .
همچنین به اندازه گیری زاویه ها و مقایسه ی دو زاویه هم می پردازیم .
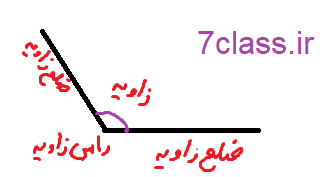
در شکل زیر یک زاویه رسم شده است و اجزای تشکیل دهنده ی آن نیز مشخصی شده است .
نام گذاری زاویه
برای نام گذاری زاویه باید به یکی از دوصورت زیر عمل می کنیم .
الف ) فقط راس زاویه را نام گذاری می کنیم .
ب) علاوه بر راس زاویه دو سر اضلاع زاویه را نیز نام گذاری می کنیم.
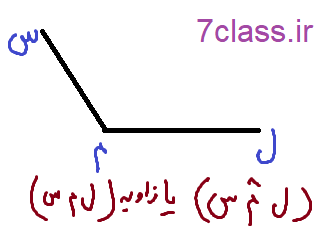
نکات نوشتن نام زاویه :
- در نوشتن نام یک زاویه با سه حرف ، نام راس حتما باید در وسط قرار داشته باشد .
- در نوشتن نام یک زاویه با سه حرف مهم نیست که نام کدام ضلع را اول نوشته باشیم
- زاویه هایی را که دارای یک ضلع و راس مشترک با زاویه ی دیگر می باشند با سه حرف می خوانیم .
- شما برای دانلود نمونه سوال ریاضی چهارم نوبت اول بر روی لینک کلیک کنید .
اندازه گیری زاویه کلاس چهارم
منظور از اندازه ی یک زاویه ، این است که ببینیم دو ضلع یک زاویه به چه میزان از یکدیگر دور یا به یکدیگر نزدیک هستند .
در واقع اندازه ی یک زاویه به مقدار باز یا بسته شدن اضلاع آن وابسته است .
به این ترتیب که هر چه اضلاع زاویه بیشتر باز شده باشند ، اندازه ی زاویه بیشتر می شود
هر چه اضلاع زاویه بسته شده باشند ، اندازه ی زاویه کمتر خواهد شد .
به عنوان نمونه در دوشکل زیر اندازه ی زاویه (ن) از اندازه ی زاویه ی (م) بیشتر است
چون (ن) بازتر از (م) است .

زاویه راست
با بررسی انواع زاویه به زاویه راست می رسیم که تشخیص راست بودن یک زاویه را به کمک گونیا می توانیم انجام دهیم .
از گونیا برای تشخیص اینکه یک زاویه راست است یا خیر می توان استفاده نمود .
به این صورت که هر دو ضلع گونیا باید بر روی ضلع زاویه شما قرار بگیرد و کاملا منطبق باشد .
زاویه تند و زاویه باز
به هر زاویه ای که از زاویه راست کوچک تر باشد ، زاویه تند می گویند .
به هر زاویه ای که از زاویه راست بزرگ تر باشد ، زاویه باز می گویند .
نکته : ۱- برای مقایسه ی زاویه تند و زاویه راست ، از گونیا استفاده می کنیم .
۲- برای مقایسه ی زاویه ی باز و زاویه ی راست ، از گونیا استفاده می کنیم .
۳- به زاویه ی تند ( حاده ) و به زاویه ی باز ( منفرجه ) و به زاویه ی راست ( قائم) نیز گفته می شود .
گونیا و انواع آن
قبلا گفتیم که از گونیا برای تشخیص اینکه یک زاویه راست است یا خیر استفاده می کنیم .
در گونیا یکی از زاویه راست و دو زاویه دیگر تند می باشند معمولا از دونوع گونیا به صورت روبه رو استفاده می شود .
دو نوع گونیا داریم گونیای (۳۰-۶۰) و گونیای (۳۰-۶۰)

مجموع زاویه های مثلث
مجموع زاویه های مثلث ۱۸۰ درجه می باشد
مجموع زاویه های چهار ضلعی هم ۳۶۰ درجه می باشد .